|
rFcTo |
rFcT(z) |
rFcTf |
|
Po |
|
|
|
P(z) |
|
rFcTo |
rFcT(z) |
rFcTf |
|
Po |
|
|
|
P(z) |
La forme de l'équation locale de conservation de l'énergie qui gouverne le processus de chauffage de l'eau par micro-ondes en régime stationnaire s'écrit :
dP(z)/dz = - rFcdT(z)/dz (1)
où P(z) et T(z) correspondent à la puissance micro-onde et à la température de l'eau à un point situé à une distance z de l'entrée, r, F, et c correspondent respectivement à la masse volumique, au débit et à la chaleur spécifique de l'eau.
Cependant, la puissance micro-onde à un point situé à une distance z de l'entrée est donnée par [4], [7] :
P(z) = Po exp{- 2 [Intégration de 0 à z] a(z') dz'} (2)
où Po et a(z') correspondent respectivement à la puissance micro-onde d'entrée et au coefficient d'absorption de l'échangeur. Pour un échangeur à eau WR 340 pour lequel e est l'épaisseur de la portion de liquide on a a(z') = ß / T(z') dans la plage de température 25 < T < 75° C où ß est la constante physique suivante :
ß = 7.35 e 230 dB.° C/m = 1.690 e dB.° C/mm = 0.194 e °C/mm où e est en mm.
En intégrant l'équation (1), on obtient :
Po + rFcTo = P(z) + rFcT(z) = rFcTf (3)
où la puissance micro-onde Po est totalement absorbée le long de l'échangeur, To et Tf correspondent respectivement aux températures d'entrée et de sortie de l'eau.
En dérivant l'équation (2), on obtient :
dP(z)/dz = - 2 ß P(z) / T(z) (4)
En soustrayant l'équation (4) de l'équation (1), on obtient :
rFcdT(z)/dz = 2 ß P(z) / T(z) (5)
Cependant, l'équation (3) donne :
P(z) / T(z) = rFcTf / T(z) - rFc (6)
En remplaçant P(z) / T(z), l'équation (5) devient :
dz = dT(z) / 2 ß {Tf / T(z) - 1} (7)
L'intégration de l'équation (7) le long de l'échangeur donne :
2ßz/To = - ln (1- d) - [ln (1- d) + d] DT/To (8)
où DT = Tf - To et
d = {T(z) - To}/DT
= DT(z)/DT
DT est relié aux paramètres
du processus par la formule : DT
= Po / rFc
En posant a(z') = ß / To, nous avons l'équation simplifiée :
2ßz*/To = - ln (1- d) (9)
où z* est la position approximative pour la valeur d
Considérons à présent un volume d'eau d'épaisseur e et de hauteur h(z) représenté sur le schéma ci-dessous :
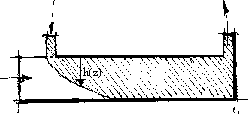
Cette variante est bien adaptée pour minimiser les réflexions sur le conduit intérieur. Le coefficient d'absorption correspondant de l'échangeur a'(z') peut être écrit de la manière suivante :
a'(z') = a(z') h(z')/b (10)
où b est la hauteur du guide d'ondes.
En suivant la même procédure que pour la portion rectangulaire, l'équation (7) devient :
h(z)dz/b = dT(z) / 2 ß {Tf / T(z) - 1} (11)
L'intégration de l'équation (11) le long de l'échangeur donne :
V(z)/v = - ln (1- d) - [ln (1- d) + d] DT/To (12)
où V(z) est le volume d'eau nécessaire conduisant à la valeur d demandée.
Par conséquent :
V(z) = [Intégration de 0 à z] eh(z')dz'
Par définition, v est le volume d'une portion liquide rectangulaire de hauteur b en un point situé à la distance To/2ß de l'entrée :
v = beTo/2ß (13)
Du fait que l'épaisseur e est sensiblement plus faible que la largeur de l'échangeur, ß varie linéairement en fonction de e [7], par conséquent v et V(z), pour une valeur donnée d, ne dépendent pas de la forme h(z) du conduit interieur.
Il est à noter que le volume V(z) est le paramètre approprié permettant de décrire le processus de chauffage par micro-ondes.