|
rFcTo |
|
rFcTf |
|
Po |
 |
|
|
|
|
|
|
rFcTo |
|
rFcTf |
|
Po |
 |
|
|
|
|
|
The form of the local energy conservation equation which governs the microwave water heating process during stady state conditions can be written as :
where P(z) and T(z) are the microwave power and the temperature of water at a distance z away from the inlet, r, F, and c are the volumetric mass, flow rate and specific heat of water respectively.
However the microwave power at a distance z away from the inlet is given by, [4], [7] :
where Po and a(z') are the input microwave power and the heat transfert absorption coefficient respectively. For a WR 340 water heat transfer for which e is the thickness of the liquid slab a(z') = ß / T(z') in the temperature range 25 < T < 75° C where ß is the following physical constant :
Integrating eqn.(1) gives :
where Po is totally absorbed along the heat transfer, To and Tf are the input and output temperatures of water respectively.
Differentiating eqn.(2) gives :
Substracting eqn.(4) from eqn.(1) yields :
However eqn.(3) gives :
Substituing P(z) / T(z), eq.(5) yields :
Integrating eqn.(7) along the heat transfer gives :
where DT = Tf - To and
d = {T(z) - To}/DT = DT(z)/DT
DT is related to the
process parameters by the formula : DT = Po / rFc
Ignoring the absorption coefficient variation with a(z') = ß / To gives the simplified equation :
where z* is the approximate position at ratio d.
Now let us consider a volume of water of thickness e and height h(z) described as follows :
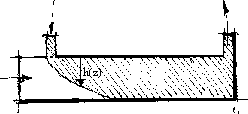
This design is well adapted to minimize microwave reflections on the inner pipe. The corresponding heat transfer absorption coefficient a'(z') can be written as:
where b is the height of the wave guide.
By following the same procedure as for the rectangular slab, eqn.(7) becomes :
Integrating eqn.(11) along the heat transfer gives :
where V(z) is the necessary volume of water which leads to the required ratio d.
Therefore :
By definition v is the volume of a rectangular liquid slab of eight b at a point distance To/2ß away from the inlet :
As the thickness e is substantially smaller than the width of the heat transfer, ß varies linearly with e [7], therefore v as well as V(z) at a given ratio d do not depend upon the shape h(z) of the inner pipe.
It will be noted that the volume V(z) is the appropriate parameter for describing the microwave heating process.